Wiskundemeisjes
Archief voor categorie 'Algemeen'
Vandaag begint een nieuw polymath project (als ik het goed begrijp om 18.00 uur onze tijd). Op initiatief van de onvolprezen Terence Tao kan iedereen meedoen aan het oplossen van de moeilijkste opgave van de Internationale wiskunde-olympiade.

Het is voor onderzoekers vooral interessant om eens te hoe zo'n polymath-probleem werkt en of de opzet bevalt (polymath wordt inmiddels ook voor serieuzere onderzoeksvragen gebruikt). En het is natuurlijk reuzeleuk om met een grote groep wiskundigen van over de hele wereld te discussiëren over de vraag of volledige inductie voor dit probleem wel een goed idee is.
Op Terences blog vind je meer informatie.
Dat lang niet iedereen van wiskunde houdt blijkt maar weer eens uit onderstaande foto + bijschrift.

Petra Visser won met deze foto de derde prijs in de wedstrijd Maak meer dan een foto, maak een verhaal, georganiseerd door Canon en de Volkskrant.
Camiel stuurde me een link naar dit mooie visuele bewijs (een van de vele die er zijn!) van de stelling van Pythagoras. "Dit had ik graag in een wiskundeles gezien," mailt hij erbij. Dus hier is het, voor alle mensen die dat ook vinden!
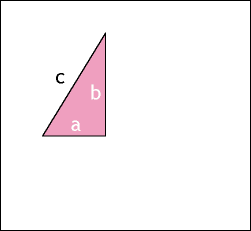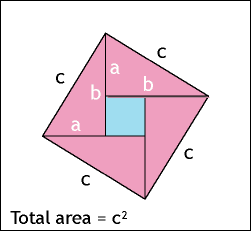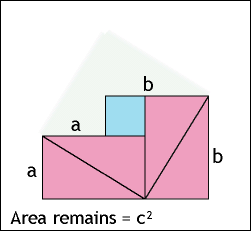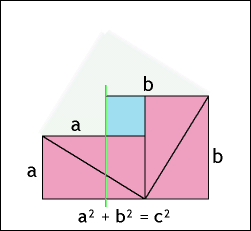
Sergio van Pul schreef voor ons een recensie van het educatieve computerspel Monkey Labs.
De eerste indruk van het spel is goed. De installatie gaat zonder moeite en wanneer je het spel start word je verwelkomd met een kleurrijk titelscherm. Hier kun je kiezen of je wilt spelen als jongen of als meisje. Heb je je keuze gemaakt dan start het spel met een kort stripverhaal om het verhaal te introduceren.

Spelstructuur
Twee jongeren stuiten bij een uitje in het bos op een geheimzinnige ingang naar een ondergronds laboratorium. In dit lab vinden ze al snel een aapje dat met een helm verbonden is aan een vreemde machine. Deze machine geeft je speelse en uitdagende rekenopdrachten, waarbij je de competitie aangaat met het aapje, dat blijkbaar erg slim is. Alleen als je van het aapje kan winnen gaat de deur naar de volgende kamer open. En zo zijn er 67 kamers om je doorheen te rekenen. Iedere kamer bevat minstens één breinmachine die de deur bedient. Maar later vind je er soms meer die andere mechanieken in de kamer regelen. Na een reeks kamers wordt je geconfronteerd met de 'Brug des Doods', waar je alleen overheen komt als je een reeks meerkeuzevragen goed beantwoordt. Het overwinnen van de brug wordt beloond met een kort stripje dat het verhaal verder uitlegt.
En dan is er nog de mysterieuze vrouw in het groen die blijkbaar ook probeert het mysterie van het laboratorium te ontrafelen.
Schuifpuzzels
Niet alleen je rekenvaardigheden worden getest. Ook je ruimtelijk inzicht, logisch verstand en vermogen om vooruit te denken worden op de proef gesteld. Het duurt niet lang voor je in een kamer komt waar de weg wordt versperd door een bad met koelvloeistof. (Blijkbaar hadden de wetenschappers in dit lab niet de beste architecten in dienst, want de kamers worden vaak half gevuld met deze dampende baden die dodelijk zijn als je er per ongeluk in valt.) Maar een aantal houten kratten biedt hulp. Door deze op een slimme manier te verschuiven kun je een brug bouwen om bij de volgende breinmachine te komen.
In eerste instantie zijn deze schuifpuzzels erg simpel. Het is een spelmechaniek dat in veel 'adventures' voorkomt en ze halen nauwelijks het niveau van vergelijkbare puzzels in een bekende spellenreeks als 'Legend of Zelda'.
Later worden er echter meer objecten toegevoegd; Schuivende platforms, dodelijke lasers, spiegels, lopende banden en schakelaars. De puzzels worden steeds uitdagender en een paar keer heb ik even rustig een paar minuten de kamer moeten bekijken om te ontdekken wat er van me verwacht werd. Gelukkig kun je een overzicht krijgen door CTRL in te drukken. Jammer alleen dat de uiterste hoeken soms buiten beeld vallen.
Rekenspelletjes
Maar dan het belangrijkste; Hoe leuk en effectief zijn die rekenspelletjes? In totaal zijn er elf verschillende spelletjes die je moet spelen, waarvan sommige variaties op elkaar zijn. Zo zijn er drie ruimtelijk-inzicht-spelletjes, 'Crazy Crates’, waarbij je een figuur van kubussen moet vergelijken met verschillende aanzichten. In de makkelijkste versie moet je het juiste aanzicht kiezen uit drie opties, terwijl de computer een blokkenfiguur opbouwt. Later moet je ook zelf aan de slag om een figuur op te bouwen of juist af te breken aan de hand van een gegeven schema. Met name de opbouwpuzzel ging in mijn geval vaak mis, omdat ik na een tijdje het overzicht over mijn bouwsel kwijt was. Je kunt de constructie niet draaien, dus is het soms moeilijk te zien hoe hoog de stapels aan de achterkant precies zijn.

Is één van jullie handig in ondertitels in een filmpje zetten? Bij mijn praatjes over wiskunde en liefde laat ik vaak een kort stukje uit A beautiful mind zien. De laatste tijd kreeg ik wat klachten dat het fragment in het Engels is en dat niet iedereen dat begrijpt. Ik heb inmiddels de ondertitels gevonden, maar het lukt me niet om ze in het filmpje te zetten. Ik wil de ondertitels graag in het fillmpje zelf hebben en ze niet via een speler mee laten draaien, omdat ik soms vanuit andere software moet presenteren. Is dit voor één van jullie misschien een peulenschilletje? Het fragment duurt trouwens maar anderhalve minuut. Ik zal een passend bedankje verzinnen!
UPDATE: Woohaa! Binnen twee minuten heeft Tim al aangeboden me te helpen, hoera!
Het is er niet helemaal de juiste maand voor, maar laatst las ik over wiskundige één-april-resultaten. Het idee is dat je een tamelijk eenvoudige bewering bewijst met overdreven ingewikkelde wiskunde. Bijvoorbeeld:
Voor alle gehele getallen \(\) is \(\) irrationaal.
Bewijs: Stel dat er positieve gehele getallen \(\) en \(\) bestaan zodat \(\). Aan beide kanten de \(\)-de macht nemen, geeft \(\). Dat betekent dat
\[\]
Dit is een tegenspraak met de door Andrew Wiles bewezen laatste stelling van Fermat. \(\)
Erg grappig, toch? Ik las over één-april-resultaten op de blog van Dick Lipton. Hij vertelt dat het idee van Faadosly Polir komt. Chapeau voor Faadosly! Kunnen jullie zelf ook een mooi voorbeeld verzinnen?
Vorige week kondigden we de bijeenkomst Huygens en de muzen aan. Op 16 mei zal Vincent Icke ons zijn nieuwe boek aanbieden, en zowel hij als wij zullen leuke dingen vertellen over Huygens en over wiskunde.
De randomgenerator van www.random.org heeft weer gesproken en de winnaar van de twee gratis toegangskaartjes is..... Ingrid! Gefeliciteerd, en tot ziens op 16 mei!
In het project Rabbitart on the move stuurt mijn vriendin Liset van Dommelen houten kunstkonijnen de hele wereld over. Ze vraagt mensen om het konijn mee te nemen op een uitje en daar een foto van naar haar te sturen. Er zwerven al heel wat konijnen rond!

Een konijn op weg naar Georgië
Liset, ook bekend als de filmster van Wiskundige zoekt vrouw, vroeg mij om voor dit project iets te vertellen over wiskunde - met een konijn op mijn rug. Omdat het project Rabbitart on the move gaat over menselijke connecties, leek het me leuk om iets te doen met sociale netwerken. Jeanine tipte me over het artikel Why your friends have more friends than you do (pdf).
Hier zie je het filmpje (het is in het Engels, zodat de konijnenliefhebbers in Georgië en Japan het ook kunnen volgen).
Dit stuk staat vandaag in de Kennisbijlage van De Volkskrant. Helaas werkt de link in dat artikel niet meer, onderaan dit stuk staat de goede link naar meer informatie.
Morgen wordt wereldwijd pi-dag gevierd. Elk jaar verzamelen pi-liefhebbers zich in de derde maand op de veertiende dag (oftewel: 3,14) voor een feestje. Tijd om de grootste misverstanden over deze wiskundige constante recht te zetten.
1. Pi heeft iets te maken met de stelling van Pythagoras.
In de kerstuitzending van Bananasplit kwam pi ter sprake. Danny de Munck gaf onmiddellijk toe dat hij niets wist van wiskunde. Naast hem zat Nance, zij had ook geen wiskundeknobbel, maar “wist nog wel dat pi de stelling van Pythagoras is”. Helaas, pi en de stelling van Pythagoras zijn de twee dingen die de meeste mensen onthouden hebben van wiskunde, maar ze hebben niets met elkaar te maken. De stelling van Pythagoras gaat over driehoeken, terwijl pi van cirkels komt. Pi is de omtrek van een cirkel gedeeld door de diameter: ongeveer 3,14. Het maakt niet uit hoe groot of klein de cirkel is, de verhouding tussen omtrek en diameter is altijd precies pi. Daarnaast verschijnt pi ook op allerlei andere plaatsen: bijvoorbeeld in de verdeling van schoenmaten.
2. Pi is precies 3,14.
Pi begint als 3,14159 en daarna volgen nog oneindig veel cijfers. In die cijfers zit geen regelmaat. In de praktijk wordt daarom altijd een benadering van pi gebruikt. In de bijbel laat Solomo voor een tempel een bekken maken: “vijf el hoog, met een middellijn van tien el en een omtrek van dertig el”. Volgens deze tekst is pi dus gelijk aan 30/10 = 3, een eenvoudige benadering. Hoe nauwkeuriger de berekening, hoe meer decimalen er nodig zijn. Pi is niet te schrijven als een breuk, maar kan wel goed benaderd worden met breuken. Op school wordt vaak 22/7 (ongeveer 3,14285) gebruikt voor pi.
3. In de Amerikaanse wet staat dat pi gelijk is aan 3.
Het is een vaak voorkomend misverstand dat een bijbelvaste Amerikaanse staat in de wet heeft vastgelegd dat pi drie is. Zoiets is nooit gebeurd of zelfs maar voorgesteld. Wel is in 1897 in Indiana een merkwaardig wetsvoorstel ingediend door een amateurwiskundige. Hij wilde pi anders definiëren om berekeningen makkelijker te maken. In zijn voorstel waren allerlei verschillende waarden voor pi te vinden, variërend van 3,2 tot 4(!). Het voorstel werd in eerste instantie unaniem aangenomen, maar het sneuvelde alsnog in de senaat. Niet omdat de senaatsleden vonden dat er iets mis was met de theorie, maar omdat ze dachten dat pi geen zaak van wetgeving was.
4. In pi zitten geheime boodschappen verstopt.
Het zoeken naar gecodeerde boodschappen in de oneindige reeks decimalen van pi is een populaire hobby. Door de cijfers om te zetten naar letters kun je zinnen als “God bestaat” in de decimalen ontdekken. Het probleem is dat wiskundigen vermoeden dat elk rijtje cijfers uiteindelijk een keer in de decimalen van pi voorkomt, dus dan zou ook de zin “God bestaat niet” vanzelf een keer in de decimalen opduiken, net als de integrale tekst van Hamlet of de Volkskrant van vandaag. Voor wie het moeilijk te geloven vindt dat in één getal alle mogelijke teksten zijn gecodeerd: er is een getal waarvan we dit zeker weten dat alle mogelijke codes er instaan. Dat is de contante van Champernowne: 0,12345678910111213141516... enzovoorts. Niets magisch aan dus.
5. Het is belangrijk om pi zo ver mogelijk uit te rekenen.
Al eeuwenlang is het een sport om zoveel mogelijk decimalen van pi uit te rekenen. Omdat het er oneindig veel zijn, valt het record steeds weer te verbeteren. Zhu Chongzi berekende bijvoorbeeld rond het jaar 500 al dat pi tussen 3,1415926 en 3,1415927 ligt. Op dit moment staat het record op 2,7 biljoen cijfers. Om een indruk te geven hoe belachelijk veel cijfers dit zijn: als je deze 2,7 biljoen cijfers gaat opzeggen (zeg één per seconde), dan duurt dat 85.616 jaar. Voor de meeste berekeningen zijn echter een stuk of tien cijfers na de komma ruim voldoende en niemand heeft meer dan duizend cijfers nodig.
Dat de records toch steeds sneuvelen heeft twee redenen. Allereerst hebben snelle rekenmethodes allerlei andere toepassingen, het uitrekenen van pi is niet meer dan een mooie test. Bovendien raakt het uitrekenen van zoveel mogelijk decimalen voor sommige mensen een obsessie. Zelfs Isaac Newton raakte in de ban van pi en schreef in 1666: “Ik schaam me om te vertellen tot hoeveel cijfers ik deze berekeningen heb uitgevoerd, toen ik niets anders te doen had.”
Tot en met 28 maart hangen de eerste miljoen decimalen van pi in de Centrale Bibiliotheek Rotterdam als onderdeel van een expositie over de geschiedenis van pi. Morgen wordt tussen 13.00 en 17.00 uur pi-dag gevierd met lezingen, wiskundige puzzels en pi-koekjes. De toegang is vrij. Adres: Bibliotheek Rotterdam, Hoogstraat 110, Rotterdam. Meer informatie op de site van de bibliotheek.
 Internetbureau Rotterdam
Internetbureau Rotterdam 

