Wiskundemeisjes

Vorige week schreef ik hier over onze jaartelling. Naast een boel reacties op de site kreeg ik ook een hele lading emails over dit onderwerp. Erg aardige emails, van vriendelijke mensen, geen wijsneuzen te bekennen. Bedankt voor al jullie reacties en verklaringen! Vooral de uitleg met rangtelwoorden en de vergelijking met een `nummering in letters’ als c, b ,a, A, B, C waren verhelderend. Toch zou ik nog steeds liever een jaartelling met het jaar nul hebben gehad, misschien doordat ik nul als het eerste natuurlijke getal zie…

Lezer Jan mailde dat het verhaal gaat dat Donald Knuth, de informaticus, ooit gezegd heeft dat de bladzijdenummering van de meeste tijdschriften verkeerd is omdat de bladzijdenummers bovenaan de bladzijde staan en met 1 (één) beginnen. Zijn stelling was: bladzijdenummers onderaan de bladzijden (van boeken etcetera) horen bij 1, maar bladzijdenummers bovenaan de bladzijde met 0 (nul) te beginnen. Kan iemand dat verhaal bevestigen?

Toevallig las ik deze week ook The Salmon of Doubt van de onvolprezen Douglas Adams. In Unfinished Business of the Century bespreekt hij één van de grote problemen van de 20ste eeuw: de tekst van “”Do-Re-Mi,” uit The Sound of Music. De tekst begint echter met iets anders…

Just a few more days to go. I think it’s important not to leave a century, let alone a millennium, without cleaning up behind you, and there is clearly unfinished business to attend to. I suggest that the Net community try to identify this unfinished business and see if, between us, we can’t get it squared away so that we can all enjoy the New Year celebrations with the sense of a century well done.

But first, a word to the pedants.

Yes, I know you all think that the millennium doesn’t change till a year later, and very tedious you are about it, too. In fact, you are so keen to have something you can wag your fingers at the rest of the world about, that you are completely missing the point. IT HAS NO SIGNIFICANCE WHATSOEVER! It is merely an excuse to go “Whoa! Look at that! There they go!” as all the digits change.

What other significance can it _possibly_ have? Ten (along with its multiples) is an arbitrary number. January 1 is an arbitrary date. And if you happen to think that the birth of Jesus Christ is a significant moment, then all we can say with any certainty is that 1 A.D. isn’t when it happened. Or 0 A.D., if the previous year had been called that (which, as we all know because the pedants keep banging on about it, it wasn’t).

Then, as the historians (a _much_ more interesting bunch than the pedants) tell us, the calendar has been played around with so many times in the intervening years anyway that the whole thing is doubly meaningless.

Consider this: we’ve only relatively recently got our time- and date-keeping precisely defined and standardised, with the aid of atomic clocks and suchlike. And on January 1, 2000 (if the doomsayers are to believed) all of our computer systems will go haywire and plunge us back in the stone age (or not, as the case may be). So it seems to me that midnight on December 31 is the only solid and reliable point we have in the entire sorry mess, and so perhaps we should be celebrating that just a little bit. And instead of saying that we have got the end of the millennium (or bi- millennium) wrong, we should say that our ancestors got the _beginning_ of it wrong, and that we’ve only just sorted the mess out before starting a new mess of our own. What the hell does it matter anyway? It’s just an excuse for a party.

Bij dat laatste sluit ik me van harte aan. Ik wens jullie allemaal een mooi feestje vanavond en vooral heel veel goeds voor 2010!

Deze column staat in de kerstbijlage van de Volkskrant.

Nog maar een paar nachtjes slapen en dan is het 2010. Eindelijk zijn we verlost van die onbestemde jaren nul. Een nieuw decennium, een nieuw geluid! Hoewel, waren er niet van die wijsneuzen die in 2000 beweerden dat het nieuwe millennium pas op 1 januari 2001 begon? Begint het nieuwe decennium dan soms ook pas volgend jaar?

Helaas hebben de wijsneuzen in dit geval gelijk: onze jaartelling loopt vanaf het jaar één en niet vanaf het jaar nul. Dus als je netjes telt, dan begint het nieuwe decennium inderdaad pas over iets meer dan een jaar. Zo is het vastgelegd en daar valt niets meer aan te veranderen. Op nieuwjaarsborrels kun je de wijsneuzen dus gelijk geven en snel over iets anders beginnen.

Bijvoorbeeld over dat het wel heel raar is dat er geen jaar nul is. Blijkbaar was het eerst één voor Christus (al waren daarvan op dat moment nogal weinig mensen op de hoogte) en daarna ineens één na Christus. Dat levert merkwaardige dingen op. Neem bijvoorbeeld een Romein die geboren werd in 10 voor Christus. In het jaar 30 na Christus werd deze man dan 39. Dat is toch een beetje vreemd. De Romein in kwestie merkte daar weinig van, want onze huidige jaartelling werd pas eeuwen later vastgelegd.

Een Romein die al genoeg aan zijn hoofd heeft

In 525 gebruikte Dionysius Exiguus voor het eerst de term Anno Domini, oftewel Het jaar des Heeren, wat wij nu aanduiden met na Christus. Exiguus bedacht het jaartelsysteem om de juiste data van Pasen te kunnen bepalen, een belangrijke zaak voor de kerk en middenstand. Hij gebruikte de telling niet voor historische gebeurtenissen en verklaarde trouwens ook niet hoe hij nou wist dat het op dat moment het jaar 525 was.

Ruim 200 jaar later gebruikte de monnik Bede als eerste een jaar vóór Christus. Hij legde toen het begin van onze jaartelling vast als het jaar één. Het lijkt een bewuste keuze te zijn geweest om de jaartelling te laten beginnen bij één en niet bij nul. Vaak wordt geopperd dat Bede domweg nooit had gehoord van het getal nul, maar dat is niet waar. Hij gebruikte regelmatig het Latijnse woord nulla (niets) waar wij nu een nul zouden schrijven.

Sindsdien gebruiken historici nooit meer het jaar nul, maar sterrenkundigen, Boeddhisten en Hindoes doen dat wel. Vaak worden de verschillende keuzes uitgelegd als het verschil tussen meten en tellen. Bij tellen begin je vanaf één, denk aan de pagina’s van een krant. Bij meten begin je vanaf nul: zoals bij een liniaal. Onze eigen leeftijd meten we dus in jaren, we beginnen te tellen vanaf nul jaar.

Het telargument bij de jaartelling snap ik zelf nooit zo goed: voordat je één iets hebt, heb je er toch nul? En geen min één? Ik kan eigenlijk geen enkel goed argument verzinnen om de jaartelling te laten beginnen bij het jaar één. Wat zie ik over het hoofd? Waarschijnlijk kan een vriendelijke wijsneus dat me haarfijn vertellen op een nieuwjaarsborrel.

Adrien-Marie Legendre (1752 – 1833) is een beroemd wiskundige. Hoewel allerlei wiskundige begrippen naar hem genoemd zijn, is er maar weinig over zijn leven bekend en werd hij in zijn eigen tijd minder hoog geacht dan nu. En zoals vaak het geval is bij historische figuren zijn er maar weinig portretten van de man bekend. Lange tijd dacht men dat hij er zo uitzag:

Maar onlangs bleek dat dit helemaal niet de wiskundige Legendre is! Peter Duren vertelt in zijn artikel Changing Faces: The Mistaken Portrait of Legendre (pdf) dat de man op dit portret de politicus Louis Legendre is. Waar komt de verwarring vandaan? Ditzelfde portret verschijnt al meer dan honderd jaar als beide personen.

Het portret van Louis Legendre verscheen in een boek in 1833, en hoewel zijn volledige naam achter in de index staat, staat onder het portret alleen zijn achternaam. Er staan ook een paar prominente wiskundigen in het boek, dus waarschijnlijk heeft iemand een keer niet zo goed opgelet en aangenomen dat het om de wiskundige ging. Daarna is het portret een eigen leven gaan leiden, ook omdat er verder geen enkel portret van de wiskunde Legendre bekend was, en iedereen die hem persoonlijk gekend had al lang overleden was.

Toen dit probleem via internet aan het licht kwam, ging men natuurlijk op zoek naar een echt portret van de wiskundige. En wonderbaarlijk genoeg is dat gelukt: in een serie karikaturen dook een karikatuur van de wiskundige Legendre op, samen met de wiskundige Fourier (zie hier). Op die karikatuur zie Legendre er zo uit, waarschijnlijk vooral om hem met de dikke en vrolijke Fourier te contrasteren:

Op de website van Gérard Michon, die de karikatuur ontdekte in een catalogus, is meer informatie over de ontdekkingstocht te vinden, maar lees dus vooral ook Durrens interessante artikel.

(Via de weblog van Dave Richeson en een tip van Tom Koornwinder.)

Een kort nieuwtje, dat eigenlijk vooral oud is: vandaag wordt door wiskundigen gevierd dat de Riemann-hypothese 150 jaar geworden is. De Riemann-hypothese is een van de bekendste grote onopgeloste wiskundeproblemen. En wie het lukt ziet een miljoen dollar tegemoet: het Clay Institute zette het probleem in 2000 op de lijst van zeven Millennium Problems. We schreven al eerder over de Riemann-hypothese: hier en hier, bijvoorbeeld.

Riemann publiceerde zijn hypothese in november 1859. Hier kun je meer lezen over zijn artikel, en ook kun je daar Riemanns originele manuscript als pdf downloaden. De eerste pagina ziet er zo uit:

Het is misschien een beetje gek om te vieren dat we iets al heel lang niet kunnen bewijzen of weerleggen, maar onopgeloste problemen zijn heel belangrijk in de wiskunde: het zoeken naar een oplossing voor zo’n groot probleem levert vaak een boel interessante wiskunde en onverwachte verbanden op, ook als de oplossing niet gevonden wordt. Allerlei wiskundigen over de hele wereld geven vandaag lezingen om de 150e verjaardag van de Riemann-hypothese te vieren. Niet hier in de buurt, helaas. Gelukkig heb ik begin november op een conferentie met mijn geschiedenis-van-de-wiskunde-collega’s al geproost op deze verjaardag van de Riemann-hypothese!

Pythagoras, het wiskundetijdschrift voor jongeren (en docenten, en andere geïnteresseerden) bestaat al een hele tijd: bijna vijftig jaar. In die vijftig jaar is er veel veranderd (en niet alleen zinnen als “Onder de goede oplossers wordt een boekenbon van ƒ2,50 verloot”) zoals je nu zelf kunt zien, want de hele eerste jaargang is vanaf nu online beschikbaar in pdf-formaat! En wat nog veel leuker is: de komende tijd zal het archief langzaam gevuld worden met pdf-files van alle oude nummers, zodat alle Pythagorassen die ooit verschenen zijn online beschikbaar komen en dus ook makkelijk te doorzoeken zullen zijn. Leuk, want er is een boel in te ontdekken!

In het meest recente boek van David Leavitt, “The Indian Clerk”, speelt wiskunde een grote rol. Het boek speelt in het begin van de twintigste eeuw en gaat over de relatie tussen de wiskundigen G. H. Hardy en Srinivasa Ramanujan. Ik ben er zelf in bezig, en het begin belooft veel goeds!

Op dinsdag 16 juni komt Leavitt naar Amsterdam. The John Adams Insitute organiseert dan samen met Uitgeverij De Harmonie een bijeenkomst over “The Indian Clerk”! De voertaal is Engels.

Tijd: 20 uur
Plaats: Posthoornkerk, Haarlemmerstraat 124-126, Amsterdam
Kaarten: via www.john-adams.nl
Prijzen: JAI-leden € 11 – Student/Senior € 10 – Niet-leden € 18,50

Het boek verschijnt in het Nederlands onder de titel “De Indische klerk”. Van de website van de uitgever:

Op een januariochtend in 1913 treft de charismatische en excentrieke G.H. Hardy, die op zijn zevenendertigste al beschouwd wordt als een van de grootste wiskundigen van zijn tijd, een mysterieuze envelop aan. Hij vindt hierin een brief van een Indische klerk, Srinivasa Ramanujan, die beweert op het punt te staan een revolutionaire wiskundige ontdekking te doen. De collega’s van Hardy menen dat hij met een oplichter van doen heeft, maar Hardy is ervan overtuigd dat de klerk serieus genomen moet worden. Deze keuze zal niet alleen zijn eigen leven en dat van zijn vrienden veranderen, maar de hele geschiedenis van de wiskunde.

“Mathematics and its paradoxes provide a deep vein of metaphor that Leavitt uses to superb effect, demonstrating how the most meaningful relationships can defy both
logic and imagination”, aldus The New Yorker.

Vorige week was ik in het Louvre. En behalve de glazen pyramides was er nog meer wiskunde te zien. Dit schilderij bijvoorbeeld: “Portret van een mathematicus” van Ferdinand Bol. Ik had met moeite zelf een foto genomen, maar die is niet zo mooi, want het schilderij hing nogal hoog en spiegelde ook nog. Gelukkig is op internet alles te vinden!

Zijn meetkundige tekening nog een beetje groter:

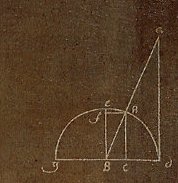
Ik heb overigens geen idee of hier een echte wiskundige uit die tijd afgebeeld is, en zo ja, wie. Iemand anders wel? Het schilderij komt uit 1658.

Zoals onlangs beloofd: iets meer over Edsger W. Dijkstra. Deze column verscheen eerder in Technisch Weekblad, vakblad voor hogeropgeleide technici en bèta’s.

Vijftig jaar geleden publiceerde Edsger Dijkstra zijn kortstepadalgoritme. Daarom een kleine ode aan de in 2002 overleden Dijkstra, iemand waar we als Nederlanders best wat trotser op mogen zijn. Dijkstra was een van de eerste programmeurs van Nederland. Toen hij in 1957 trouwde, werd het beroep computerprogrammeur door de burgerlijke stand nog niet erkend en uiteindelijk gaf hij maar `theoretische natuurkundige’ op.

Zijn beroemdste resultaat is het kortstepadalgoritme, dat de kortste verbinding vindt tussen twee knopen in een graaf (een verzameling punten waarvan sommigen verbonden zijn). Denk bijvoorbeeld aan het vinden van de kortste route tussen twee steden. Het slimme van Dijkstra’s algoritme is dat het niet alle mogelijke routes met elkaar vergelijkt, maar dat het stap voor stap de kortst mogelijke afstanden tot elk punt opbouwt. In de eerste stap kijk je naar alle punten die vanaf het beginpunt te bereiken zijn en markeer je al die punten met de afstand tot het beginpunt. Daarna kijk je steeds vanaf het punt dat op dat moment de kortste afstand heeft tot het beginpunt naar alle punten die je vanaf daar kunt bereiken. Als je een buurpunt via een nieuwe verbinding op een snellere manier kunt bereiken, schrijf je de nieuwe, kortere afstand tot het beginpunt bij zo’n punt. Zo ga je steeds een stukje verder tot je alle punten hebt gehad en je de kortste route tot het eindpunt hebt gevonden.

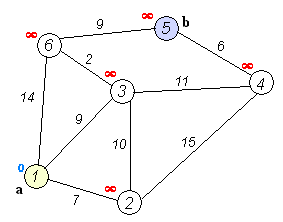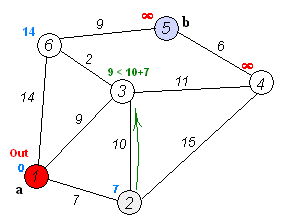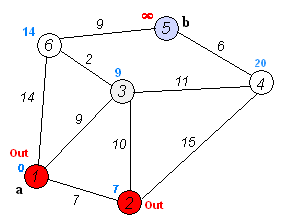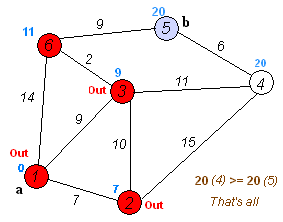
Als je het algoritme even op een servetje probeert, dan is is het zo eenvoudig dat je je afvraagt waarom je het niet zelf hebt bedacht. Dijkstra vond het zelf ook een beetje gek dat zijn naam en faam voor een groot deel gebaseerd waren op een algoritme dat hij bedacht als demonstratie voor een computer. Hij bedacht het kortstepadalgoritme zonder pen of papier op een zonnig terras terwijl hij met zijn vrouw een kopje koffie dronk.

Dijkstra verzon nog veel meer dan dit algoritme en hij had ook sterke visie op wat informatica zou moeten zijn. Honderden brieven, essays en andere handgeschreven teksten van Dijkstra staan op internet (E. W. Dijkstra Archive). Elke tekst heeft de code EWD (van Edsger W. Dijkstra) en een nummer, EWD1213 is bijvoorbeeld een inleiding bij een cursus analyse. De manier waarop hij zijn studenten daarin toespreekt, is prachtig:

It is not my purpose to “transfer knowledge” to you that, subsequently, you can forget again. My purpose is no less than to effectuate in each of you a noticeable, irreversable change. [...] I mean, if 10 years from now, when you are doing something quick and dirty, you suddenly visualize that I am looking over your shoulders and say to yourself “Dijkstra would not have liked this.”, well, that would be enough immortality for me.

Zou het hem ooit gelukt zijn dit te bereiken bij zijn studenten? De komende weken zal ik in elk geval schuldbewust aan Dijkstra denken als ik een lompe brute-force-oplossing gebruik.

Het is weer tijd voor een nieuwe aflevering van onze rubriek over wiskundigen die op een opvallende manier om het leven zijn gekomen. Deze editie gaat over Gerhard Gentzen die aan het eind van de Tweede Wereldoorlog overleed.

Gentzen werd in 1909 geboren in Duitsland. Zijn vader was een advocaat die sneuvelde in de Eerste Wereldoorlog. Gentzen kon goed leren, bij zijn eindexamen was zelfs hij de beste van zijn school. Hij kreeg een beurs om naar de universiteit te gaan en studeerde, zoals in de tijd gebruikelijk was, aan verschillende universiteiten. In 1933 haalde hij zijn doctoraat bij Weyl in Göttingen. Een jaar later werd hij de assistent van Hilbert (van het hotel en de problemen). In de tussentijd was hij ook lid geworden van de Sturmabteilung.

Gentzen werkte aan de grondslagen van de wiskunde. Onder Hilbert werkte hij aan het axiomatiseren van de wiskunde. In diezelfde tijd bewees Gödel zijn onvolledigheidsstelling. Gentzen was eerst ongerust dat dit gevolgen had voor zijn werk, maar later schreef hij dat het resultaat van Gödel erg interessant, maar niet alarmerend was:

Man kann es auch so ausdrücken, dass sich für die Zahlentheorie kein ein für allemal ausreichendes System von Schlußweisen angeben lässt, sondern dass vielmehr immer wieder Sätze gefunden werden können, deren Beweise neuartige Schlußweisen erfordern.

Het artikel over Gentzens belangrijkste resultaat op wikipedia (Gentzen’s consistency proof) heeft trouwens een expert nodig, zijn er vrijwilligers?

Gentzen was sinds 1937 lid van de NSDAP en schreef voor het nationaal-socialistische tijdschrift “Deutsche Mathematik” (bovenstaand citaat komt daaruit). Tot 1943 bleef hij verbonden aan de universiteit van Göttingen, hoewel hij tussen 1939 en 1941 in militaire dienst moest. Na zijn habilitation in 1943 vertrok hij naar Praag om daar aan de universiteit les te gaan geven – wat een deel was van het Duitse oorlogsplan. Op 5 mei 1945 kwam de Praagse bevolking in opstand en Gentzen werd, zoals alle Duitsers in Praag, gevangen genomen. Na vier dagen kwamen de Russische troepen die Gentzen onder embarlijke omstandigheden opsloten. Een medegevangene vertelde dat Gentzen best tevreden was over de opsluiting:

I can see him lying on his wooden bunk thinking all day about the mathematical problems that preoccupied him. He once confided in me that he was really quite content since now he had at last time to think about a consistency proof for analysis…

Na drie maanden in gevangenschap stierf Gentzen aan ondervoeding.

We schreven al eerder over Andrew Wiles en zijn bewijs van de beroemde laatste stelling van Fermat. Nu vond ik op Google Video de BBC-documentaire van Simon Singh en John Lynch uit 1996 over Wiles en zijn zoektocht naar het bewijs! Later verwerkte Singh het materiaal tot zijn mooie boek Fermat’s Last Theorem, vertaald als Het laatste raadsel van Fermat.

Singh heeft op zijn site een Fermat-hoekje ingericht, waar ook allerlei Fermat-trivia te vinden zijn.