Wiskundemeisjes

Zoals jullie weten vinden wij stichting Vierkant voor Wiskunde een bijzonder sympathieke organisatie. Ik ben zelf al jaren begeleider bij de wiskundige zomerkampen voor scholieren die de stichting organiseert. Daarom wil ik deze vacature graag onder jullie aandacht brengen!

De volledige vacaturetekst vind je hier.

Via de interessante lijst 100 Incredible Lectures from the World’s Top Scientists ontdekte ik een reeks colleges Kansrekenen voor levenswetenschappen. De colleges zijn gegeven door Herbert Enderton van de UCLA. Wat ik heb gezien, vond ik erg goed! Hieronder het eerste college, de rest van de reeks staat netjes bij elkaar op YouTube.

Geweldig dat topuniversiteiten dit soort collegereeksen online zetten (er is nog veel meer moois te vinden) en dat iedereen ter wereld dit gratis mag kijken. Wel grappig trouwens: het eerste college is ruim 26.000 keer bekeken, het tweede nog maar 4600 keer en het laatste college "slechts" 882 keer. Nuja, de laatste keer dat ik een collegezaal met ruim 800 studenten zag was...eh...nooit.

Zoals jullie inmiddels wel weten is de Riemann-hypothese een van de grote onopgeloste problemen in de wiskunde. Pas schreven we nog dat de hypothese 150 jaar geleden geformuleerd werd.

Er is goed nieuws voor iedereen die in 5 of 6 VWO zit en wiskunde B1,2 volgt: de webklas over de Riemann-hypothese van de UvA, begeleid door Jan van de Craats, gaat weer van start! Een webklas duurt ongeveer tien uur, verdeeld over vier weken, en gebeurt helemaal online. De omschrijving van de website:

De Riemann-hypothese is het belangrijkste open probleem van de wiskunde. Als je dat oplost, word je wereldberoemd, en bovendien verdien je de prijs van één miljoen dollar die er voor is uitgeloofd.

De Riemann-hypothese heeft te maken met de rij van alle priemgetallen, de gehele getallen groter dan 1 die alleen maar deelbaar zijn door 1 en door zichzelf: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ….

Hoe liggen de priemgetallen verspreid tussen de andere getallen? Hoeveel priemgetallen zijn er? Hoeveel priemgetallen zijn er van honderd cijfers? Van duizend cijfers? Bernhard Riemann schreef hierover in 1859 een baanbrekend artikel. Daarin formuleerde hij ook zijn beroemde vermoeden, min of meer als een losse opmerking terzijde. Maar niemand heeft het nog kunnen oplossen.

In deze webklas leer je van alles over priemgetallen. Maar ook over complexe getallen, oneindige rijen, oneindige reeksen en oneindige producten. En over differentiëren en integreren. Je maakt kennis met de meest fantastische en uitdagende stukken wiskunde die er zijn.

Verdere informatie en de mogelijkheid om je aan te melden vind je hier (en klik door in de linkerbalk naar "Meedoen" en "Webklas kiezen").

Al maanden geleden ontving ik een prachtig boekje van een Puzzelwandeling door historisch Nijmegen. Ik bedacht dat het leuk was om die wandeling zelf te maken voor ik er een stukje over schreef. Naïef als altijd dacht ik dat ik daar tijd genoeg voor had. Ik vergat even dat ik in die maanden mijn proefschrift af moest maken, terwijl ik al een nieuwe baan had en daarnaast freelance werk deed. Tel erbij op dat ik ook nog tien uur per nacht slaap nodig heb en dat zoals Wieb Bosma altijd zegt "de rest van Nederland nogal afgelegen ligt ten opzichte van Nijmegen". Kortom: ik ben nog steeds niet naar Nijmegen geweest, maar het is hoog tijd om iets over deze wandeling te schrijven. Dan kunnen lezers die in buurt van Nijmegen wonen (of die iets beter zijn in tijd-management) snel op een leuk uitje.

De wandeling is 6 km lang en duurt volgens de makers ongeveer 5 uur (ik gok dat je een flink deel van die tijd al puzzelend op terrasjes of in cafés doorbrengt). In het boekje staat informatie over de geschiedenis van Nijmegen en de gebouwen die je ziet. En natuurlijk een heleboel puzzelvragen. Dit is een voorbeeld van zo'n vraag.

De Sint Nicolaaskapel is het oudste gebouw van Nijmegen en een van de oudste van Nederland. Het werd omstreeks 1030 gebouwd en maakte deel uit van een grote burcht die de Duitse keizer Frederik Barbarossa in de 12de eeuw op het Valkhof liet bouwen. Het is een voorbeeld van Byzantijnse bouw. De centrale toren is achthoekig. Daaromheen is het gebouw zestienhoekig. Aan het dak is deze structuur goed te zien.

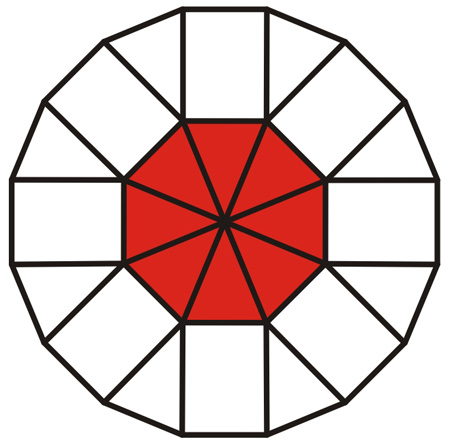
De acht- en zestienhoek zijn regelmatig. De omtrek van de zestienhoek is groter dan de omtrek van de rode driehoek. Hoeveel keer zo groot?
1 meer dan 2 keer
2. precies 2 keer
3. minder dan 2 keer

De oppervlakte van de witte ring van de zestienhoek is groter dan de oppervlakte van de rode achthoek. Hoeveel keer zo groot?
4. meer dan 3 keer
5. precies 3 keer
6. minder dan 3 keer

De wandeling is gemaakt door Leon van den Broek (onder andere bekend als organisator van Kangoeroe) en wiskundeleraar Lambert Kemerink. Op de site Puzzelwandeling Nijmegen vind je meer informatie. Het boekje is te koop voor 3 euro bij boekhandels en VVV in Nijmegen. Je kunt het boekje ook bestellen via de site.

Leen tipte ons dat wiskundemeisje Danica McKellar eergisteren een gastrol speelde in The Big Bang Theory (dé sitcom voor nerds). Zelf kijk ik al een tijdje niet meer naar die serie, maar deze aflevering (titel "The Psychic Vortex") heb ik toch even gekeken. Mmm...niet echt een glansrol voor Danica, ze mocht niet eens een grap over Flatland maken...

De veiligheid van cryptosysteem RSA is gebaseerd op het feit dat het moeilijk is om heel grote getallen te ontbinden in priemfactoren. Bij RSA wordt altijd een heel groot getal gebruikt dat het product is van twee (ook grote) priemfactoren, en als je erachter kunt komen wat die priemfactoren zijn, kun je de boodschappen die met behulp van dat grote getal versleuteld zijn lezen. Dat is natuurlijk niet de bedoeling.

Een internationaal team van onderzoekers, waaronder wiskundigen van het CWI, is er nu in geslaagd zo'n groot getal te factoriseren: het RSA-getal RSA-768. Het is een getal van 232 decimale cijfers. Dit getal was een van de getallen uit de RSA Factoring Challenge. In 1991 werd een rits getallen gepubliceerd; elk van die getallen was gemaakt door twee heel grote priemgetallen met elkaar te vermenigvuldigen. De uitdaging was natuurlijk om deze priemfactoren te vinden. In 2007 werd een eind gemaakt aan de RSA Factoring Challenge, maar nog niet alle getallen zijn gefactoriseerd.

Betekent het feit dat we steeds grotere getallen kunnen factoriseren dat RSA niet meer veilig is? Nee hoor, maar in de keuze van de sleutels moeten wel steeds grotere getallen gebruikt worden.

Lees hier een stukje van Koen Vervloesem over deze prestatie, en lees hier het persbericht van het CWI.

(Met dank aan Jurjen voor de tip.)

Deze column staat vandaag in de Volkskrant.

Het nieuwe jaar is net begonnen. Hoe staat het met uw goede voornemens? De mijne hebben dit jaar vooral met werk te maken (mijn proefschrift eindelijk afmaken, bijvoorbeeld), maar een van de meest voorkomende goede voornemens is een paar kilo afvallen.

Volgens de laatste cijfers van het CBS had in 2008 maar liefst 46,9 procent van de Nederlanders van twintig jaar of ouder overgewicht. Hierbij is overgewicht gedefinieerd met behulp van de zogenaamde Body Mass Index (BMI): je BMI is je gewicht gedeeld door het kwadraat van je lengte, waarbij je je gewicht in kilogrammen en je lengte in meters moet invullen. Wie 60 kilo weegt en 1 meter 67 lang is, heeft een BMI gelijk aan 60/(1,67)² = 21,5.

Je hebt overgewicht als je een BMI hebt van 25 of meer. Met een BMI tussen de 25 en 30 heb je matig overgewicht, en bij een BMI van 30 of meer heb je ernstig overgewicht. Je hebt ondergewicht als je BMI kleiner is dan 18,5.

Maar wat betekent dat getal nou eigenlijk? Het is een heel rare grootheid: je deelt je gewicht (je massa, eigenlijk) door het kwadraat van een lengte. De bijbehorende eenheid is dus kg/m². Fysiologisch gezien betekent deze grootheid helemaal niets, de BMI meet geen echt bestaande eigenschap van je lichaam.

Een ander probleem is dat de index geen rekening houdt met lichaamsbouw en vetpercentages. Een atletisch persoon met veel spieren en weinig vet is relatief zwaar en heeft een hoge BMI, want spieren hebben een hogere dichtheid dan vet. Toch wil je eigenlijk niet zeggen dat zo iemand overgewicht heeft. Ook hoe het vet over je lichaam verdeeld is, wat wel uitmaakt voor de gezondheidsrisico’s, wordt niet meegenomen in de BMI.

Waar komt die BMI dan eigenlijk vandaan?

De BMI wordt ook wel queteletindex genoemd, naar de wiskundige en sterrenkundige Adolphe Jacques Quételet (1796 – 1874). Hij was een van de eersten die statistische methoden gebruikte voor sociale fenomenen zoals criminaliteit en sterftecijfers. Daarvóór werd statistiek eigenlijk alleen maar in de sterrenkunde gebruikt.

Adolphe Quételet

Quételet probeerde aan de hand van metingen gegevens over “de gemiddelde mens” te verkrijgen. Hij verzamelde gegevens van een heleboel mensen en stelde een relatie vast tussen lengte en gewicht. In de Engelse versie van zijn boek staat: “the weight is in proportion to the square of the stature”, in andere woorden: over de hele populatie genomen staat het gewicht zo’n beetje in een vaste verhouding tot het kwadraat van de lengte.

In 1972 werd de queteletindex door Ancel Keys, die de invloed van voeding op gezondheid onderzocht, omgedoopt tot de Body Mass Index. Hij linkte de formule wel aan overgewicht, maar stelde ook dat de BMI alleen geschikt is voor populatiestudies en niet als diagnostisch instrument voor individuen.

Toch wordt de index daar veel voor gebruikt, vooral omdat hij zo gemakkelijk te berekenen is. Maar of je nu een officieel gezonde BMI hebt of niet: als je broeken sinds de Kerst wat strakker zitten, kan goede voornemens maken geen kwaad.

Tanya Khovanova verzon de volgende, tamelijk briljante, puzzel. Welke figuur hoort niet in dit rijtje thuis?

Denk goed na voor je antwoord geeft! Hier vind je de oorspronkelijke puzzel van Tanya en hier staat haar analyse van de reacties die ze kreeg.

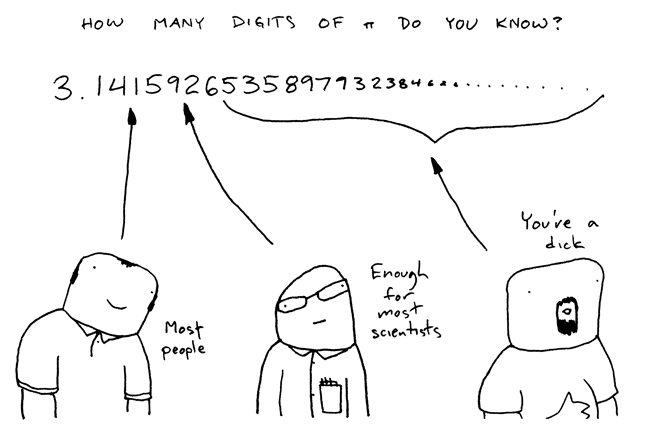
Fabrice Bellard heeft van de eerste 2,7 biljoen cijfers na de komma uitgerekend. Hoera voor Fabrice, want dat is een nieuw record! Om een indruk te geven hoeveel belachelijk veel cijfers dit zijn: als je deze 2,7 biljoen cijfers gaat opzeggen (zeg één per seconde), dan duurt dat 85.616 jaar. Dus.

Extra stoer is dat Fabrice Bellard een slimme manier verzon om de berekeningen te doen en dat hij ze op een gewone computer deed (en niet zoals vaak bij dit soort records op een supercomputer). Op zijn website beantwoordt hij vragen als "Waarom doe je dit?".

Kunnen jullie je dat mooie speelkaartenveelvlak, dat je ook zelf kon gaan knutselen, nog herinneren? Nou, Ilse Calis ging inderdaad aan de slag met de Kerst. Ze knutselde het veelvlak van zestig witte kaartjes, en ze maakte er heel creatief een lamp van. Mooi zeg, wat een goed idee!